Fuentes de Información:
http://navarrof.orgfree.com/Docencia/MatematicasII/solidosrev.htm
https://www.vitutor.com/integrales/definidas/regla_barrow.html

Problemas de aplicación de la integral 

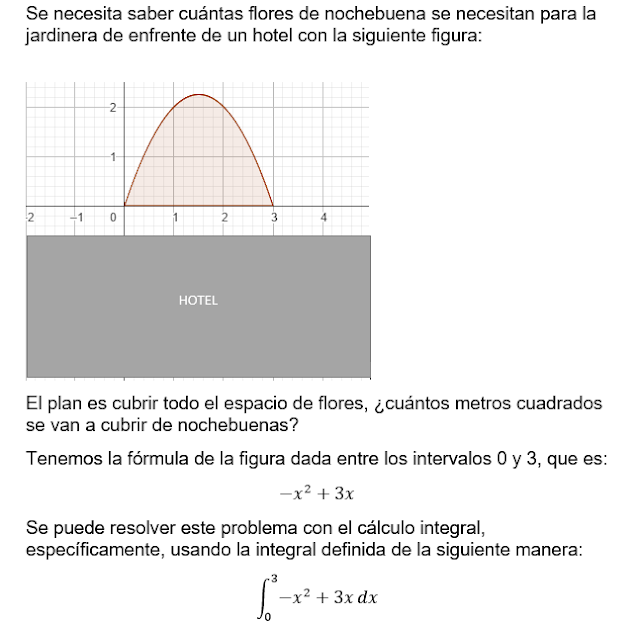
La integral definida es de mucha utilidad cuando se quiere sacar el área de una figura que no es específica, como la de la imagen, el procedimiento hace referencia a una fórmula de áreas, adaptada a un intervalo, que quiere decir: debajo de esta curva, entre estos números, voy a determinar el área.

Ejemplos de sólidos de revolución

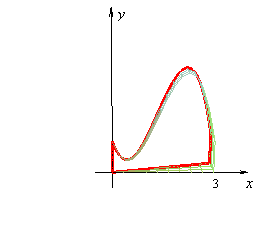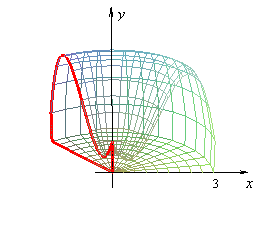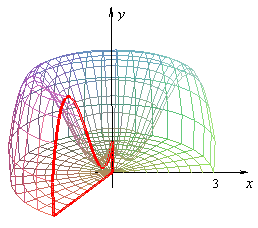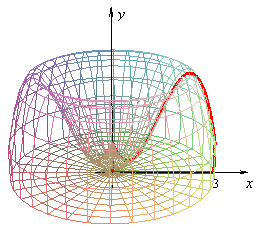
Volumen de los sólidos de revolución.

El volumen de los sólidos generados por revolución alrededor de los ejes cartesianos se puede obtener mediante las siguientes ecuaciones que contienen las integrales definidas: 

Esta fórmula proviene de la fórmula para sacar el volumen de un cilindro; si analizamos los elementos podremos darnos cuenta, veamos: 

V = π R² h

Se mantiene la constante pi (π), la R, corresponde al Radio, en este casi, nuestro radio, o conjunto de radios es f(x). y la h de la altura es dx. 

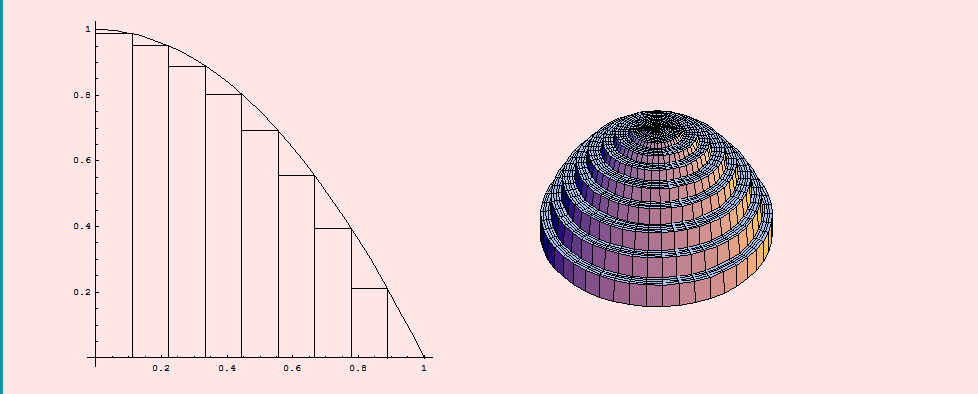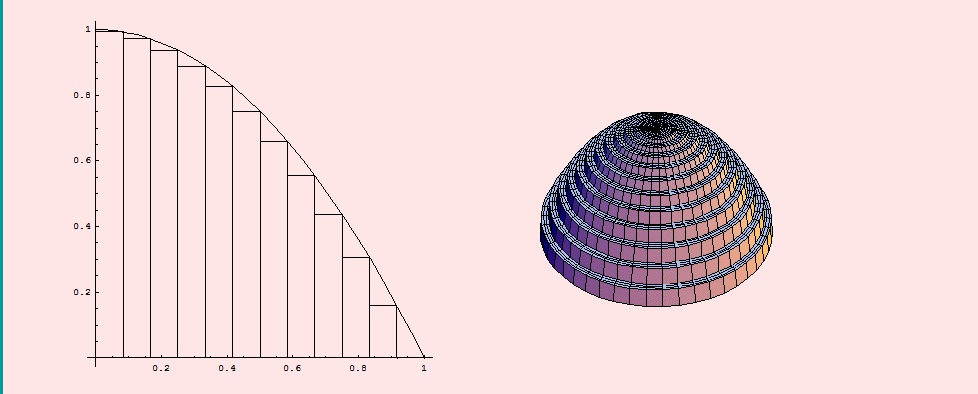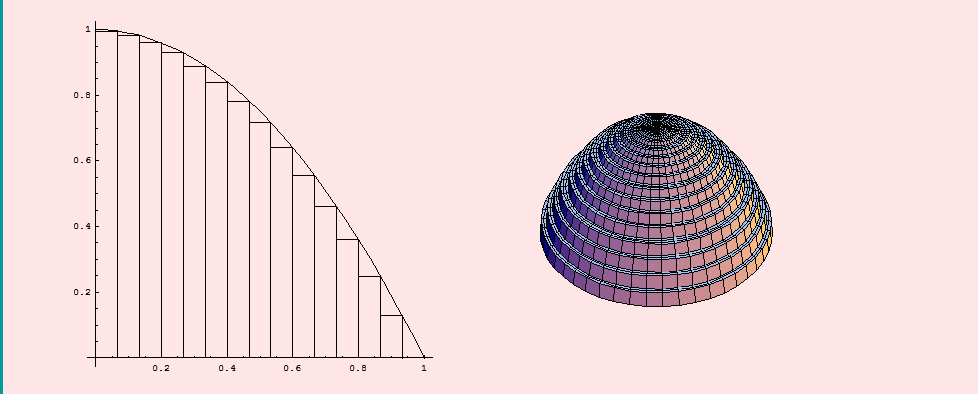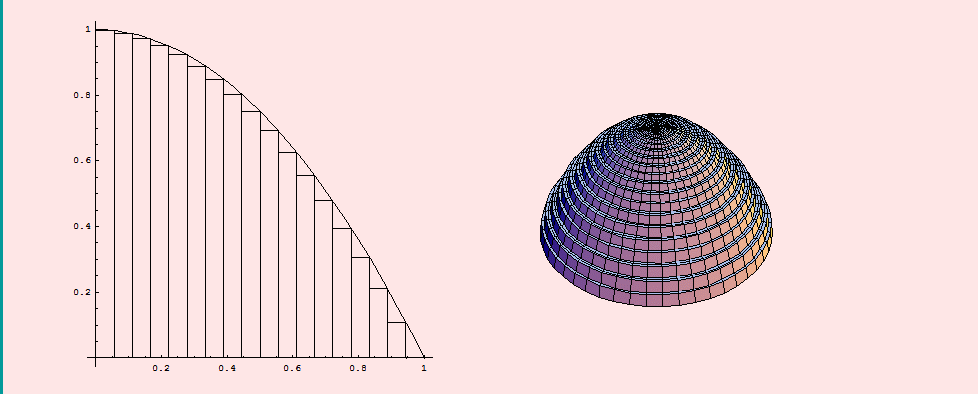
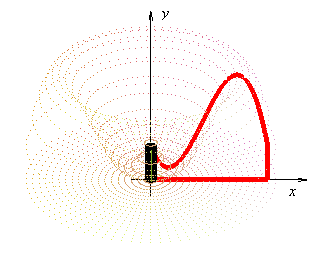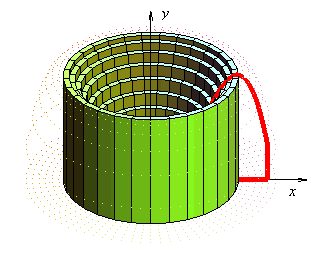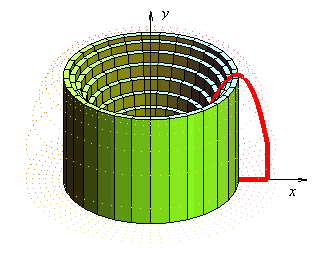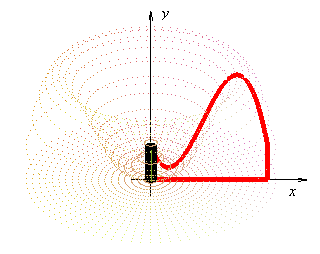
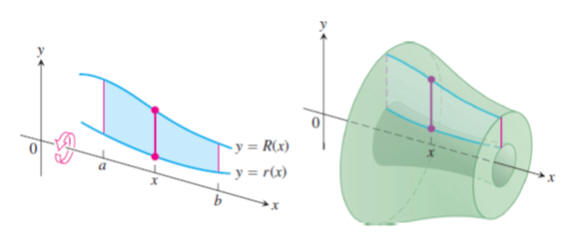
Porque lo que tienen los sólidos de revolución es que son cilindros con radios diferentes a lo largo de la altura: 

Sólido de revolución

Un sólido de revolución es un cuerpo que puede obtenerse mediante una operación geométrica de rotación de una superficie plana alrededor de una recta que esté contenida en su mismo plano. Esto se ilustra en la siguiente animación: